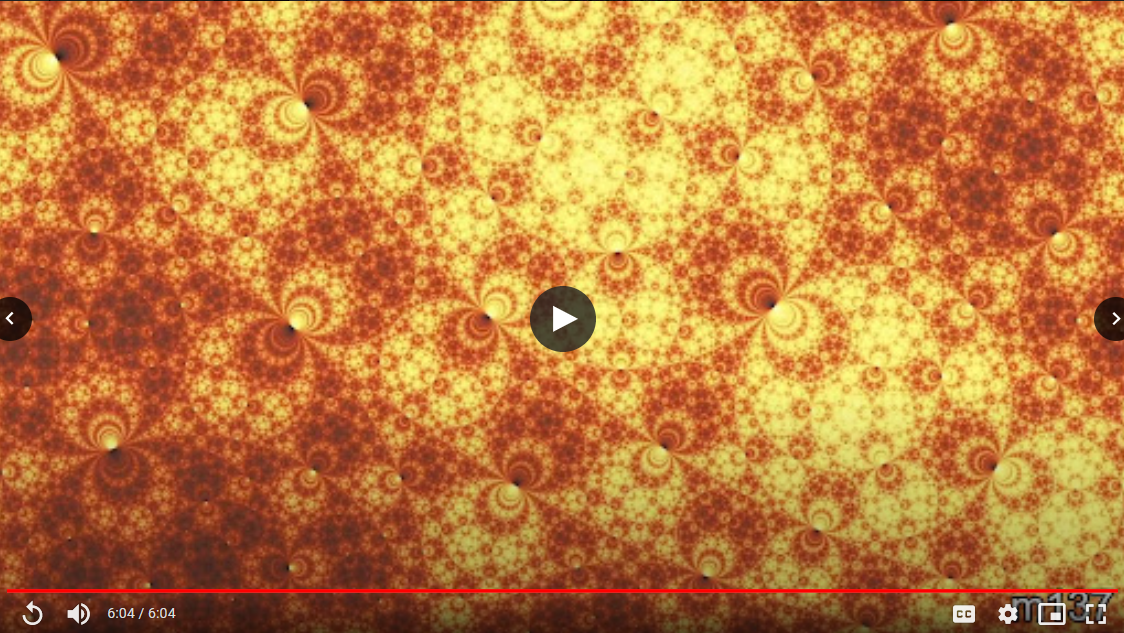
The universe may be finite. If true, then if you travel in a spaceship in one direction long enough you’ll eventually return to your start, analogous to what happens when traveling along the surface of the Earth. Such a finite universe has many possible shapes, and each possibility is called a 3-manifold. 

The set off all infinite rays emanating from some origin point in a 3-manifold forms a sphere, like the circle of the horizon when looking around you from a point on the surface of the Earth. This is called the sphere at infinity. 

Some 3-manifolds contain special surfaces (analogous to the equator on a sphere). A ray emanating from the origin point can be colored according to how often it intersects such a surface. In this way, we can assign a color to each point of the sphere at infinity to obtain a cohomology fractal. 

Cohomology Fractal s776 (2019) shows a piece of the sphere at infinity for the 3-manifold s776. This work is derived from an image generated from joint work with Henry Segerman and Saul Schleimer. 

For each knot you can tie, there is an associated 3-manifold. These particular kinds of 3-manifolds have special surfaces coming from the shape of a soap film that spans the knot. Lifting the Figure Eight Knot (2018) simultaneously shows the cohomology fractal on the sphere at infinity coming from the spanning surface for the ``figure eight knot," as well as the surface itself inside of the sphere at infinity. This piece is based on joint work with Henry Segerman